My dissertation research dedicates to maximize modeling potentials of PDE techniques for graphical models. I have proposed a general PDE-based modeling paradigm that employs elliptic and parabolic PDEs with numerical techniques for geometric and physics-based shape modeling and manipulation. I presented an integrated framework that can model graphical objects of commonly used geometric representations, such as parametric models, polygonal meshes, and implicit functions. The prototype modeling and design system I developed can provide users powerful and intuitive sculpting toolkits for geometric objects. It offers modeling features of both explicit and implicit representations. The applications include object design from arbitrary curve sketches, model reconstruction from unorganized scattered data points, interactive shape sculpting for geometric surfaces and displacement models with physical properties, direct and free-form solid manipulation and deformation, implicit objects modeling with intuitive local operations, as well as medial axis extraction of arbitrary topological meshes and skeleton-based shape manipulation and recovery by diffusion-based front propagation techniques. The system allows users to design and manipulate geometric objects intuitively without worrying about the underlying mathematical and physical details.

PDE-Based Free-Form Deformation
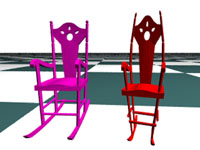
The solid elliptic PDE offers free-form deformation of solid objects because it governs the entire 3D parametric domain and provides a natural mapping between parametric and physical space. PDEs can also model implicit shapes defined on scalar intensity fields. To take advantages PDE techniques for both parametric models and implicit objects, we present an approach integrating parametric and implicit PDEs to define the solid geometry with physical properties and intensity distributions of objects subject to flexible boundary conditions. The integrated formulation of second-order or fourth-order elliptic PDEs and the associated dynamic principle permit designers to model and deform PDE solids with various degrees of freedom. Users can easily model and interact with solids of complex geometry and/or arbitrary topology from locally-defined PDE primitives through direct manipulation and free-form modeling and deformation. We employ the finite-difference discretization and the multi-grid subdivision to solve the PDEs numerically. Our PDE solid modeling system offers users various sculpting toolkits for solid design and manipulation, which allow them to interactively modify physical and geometric properties of arbitrary points, curve spans, regions on boundary surfaces and any interior parts of solid objects. Furthermore, the integration of implicit intensity information with solid geometry offers more general and arbitrary shape blending and free-form modeling and deformation for PDE solids with intensity attributes than pure geometric models. The physics-based PDE solid formulation and its associated dynamic principle permit designers to directly deform PDE solids whose behaviors are natural and intuitive subject to imposed constraints. Users can easily model and interact with solids of complicated geometry and/or arbitrary topology from locally defined PDE primitives.

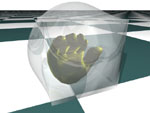Medial Axis and Skeleton Extraction and Shape Manipulation Using PDEs
We proposed a novel technique that uses diffusion equations to approximate medial axes of arbitrary 3D objects represented by polygonal meshes. The medial axis extraction process can be visually displayed by solving the time dependent diffusion equations. Furthermore, diffusion-based front propagation models governed by diffusion equations were used to recover the original data from the medial axis/skeleton and design general sweeping objects. This will greatly improve the time performance of shape manipulation and animation of complex objects by deforming the skeletons first and reconstruct the corresponding objects accordingly.

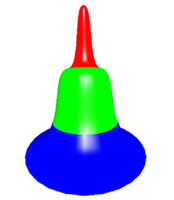
Implicit PDE Shape Modeling
Implicit functions offer modeling advantages such as arbitrary topology, collision detection, free of parametric correspondence, etc. Our implicit PDE formulation provides properties of both PDE methods and implicit functions. The implicit PDE model has the capability to reconstruct a complete model from partial information such as sketch curves, scattered points and damaged datasets. It facilitates the direct manipulation of underlying volumetric datasets via sketch curves, iso-surface sculpting, deformation of arbitrary interior regions, as well as a set of CSG operations inside the working space. It allows designers to interactively sketch the curve outlines of the object and directly manipulate implicit PDE objects. Its applications include sketch-based shape design, model reconstruction, damaged data recovery, as well as shape blending.

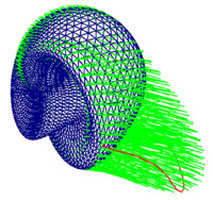
Physics-Based PDE Surfaces
PDE techniques can recover entire geometric surfaces with high continuity by given boundary information, which alleviates the burden for tedious specification over entire surface domain. The PDE surface modeling is able to model parametric surface, polygonal meshes, and surface displacements using an elliptic PDE formulation with integrated physical properties. It allows interactive design of surfaces of flexible topology as PDE surfaces or PDE displacements on the original surfaces using generalized boundary conditions and a variety of geometric and physical constraints. It supports various interactive techniques beyond the conventional boundary control including direct and local sculpting on physics-based PDE surfaces/displacements in an intuitive and physically meaningful way.